Curiosidades

Como os números complexos são aplicados em eletrotécnica


 



Acima apresentamos os quatro quadrantes trigonométricos. Veja a posição do ângulo do vetor


1° Quadrante: 0° < 90°


2° Quadrante: 90° < 180°


3° Quadrante: 180° < 270°


4° Quadrante: 270° < 360° = 0°


Devemos que o eixo x ou R deverá ser representado como o Eixo dos n°s reais. Já o eixo y ou J, representaremos o eixo dos n°s imaginários. Observe que - 45° = 315°. Um ângulo negativo na verdade, corresponde a 360°, uma volta completa, no sentido anti-horário, menos o dito ângulo. No ângulo negativo, você parte do 0°, girando no sentido horário, e no ângulo positivo, você parte do 0°, no sentido anti-horário. Assim, o ângulo de 315°, no sentido anti-horário, é a mesma posição de -45°, no sentido horário.

Representações de um Vetor.

> Forma Polar: |E| |_Ø__

> Forma trigonométrica: |E| x cos Ø + J |E| x sen Ø

> Forma cartesiana: Ex + J Ey

É importante ressaltar que estas formas representam um mesmo vetor. Com qualquer uma chegamos as outras.

|E| ---> módulo

Ø ---> ângulo

Ex ---> Parte Real (coordenada no eixo x)

Ey ---> Parte imaginária (coordenada no eixo y)

Fazendo a transformação de polar para cartesiana e vice-versa

Polar para Cartesiana:
|E| |_Ø__ ---> |E| x cos Ø + J |E| x sin Ø ---> Ex + J Ey
Ex 1: Vetor: 5 |36,87° ---> 5 x cos 36,87° + J 5 x sin 36,87° = 4 + J3
Desta forma; 5 | 36,87° = 4 + J3
Desta forma, observamos que passa-se pela forma trigonométrica para chegar a forma cartesiana.
Cartesiana para Polar:

Ex + J Ey ---> |E| = raí quadrada de ( Ex2 + Ey2 ) e Ø = arc tg Imaginário(Ey) / Real ( EX)

Video Aula - numeros complexos

www.youtube.com/watch?v=pOCUumUAkhA

www.youtube.com/watch?v=oZHb6A-Ot2o

www.youtube.com/watch?v=7yDNB7iAg-U

Aplicação de numeros complexos 1ª parte

Conjunto

Em todo o ensino médio estudamos apenas os seguintes conjuntos numéricos:
Conjunto dos naturais
Conjunto dos inteiros
Conjunto dos racionais
Conjunto dos irracionais
Conjunto dos reais

No ensino médio estudamos um novo conjunto, o conjunto dos números complexos.
Veja uma breve explicação da evolução dos conjuntos numéricos.

Iniciamos o estudo dos conjuntos numéricos pelo conjunto dos naturais representado pela letra N maiúscula, os números que pertencem a esse conjunto são:
N = {0,1,2,3,4,5,6,7,8,9,10,11, ...}.

As operações se tornaram complicadas e sem solução, pois como podemos retirar uma quantidade maior de outra menor? Então foi notada a necessidade de mais números e surgiram os números inteiros representados pela letra Z maiúscula. Os números que pertencem a esse conjunto são:
Z = {... , -3,-2,-1,0,1,2,3, ... }.

Novamente as operações se complicaram, pois ao dividirmos, por exemplo, 2: 5 não chegaríamos a uma resposta inteira, então sugiram os números que podem ser escritos em forma de fração, que são representados pela letra Q maiúscula, esses números são:
Q = { ... , -5; ...; - 4,2; ... ; - 2; ... ; -1;...; 0; ...; 3,56; ...; 4; ... } .

Podemos dizer que o conjunto dos naturais está contido no conjunto dos inteiros e racionais, que o conjunto dos inteiros está contido dentro do conjunto dos racionais, veja essa relação em forma de diagrama:


 Ao resolvermos a raiz de alguns números percebemos que as soluções encontradas eram números decimais infinitos e que não obedeciam a uma seqüência, portanto, esses números iriam participar de um conjunto chamado irracionais, representados pela letra I maiúscula. Esse conjunto fica à parte, ele e nenhum dos outros conjuntos citados acima está contido no conjunto dos irracionais.

A união dos conjuntos racionais com os irracionais forma o conjunto dos reais, representado pela letra R maiúscula, veja o diagrama abaixo:



Nem esses conjuntos satisfizeram alguns cálculos, então foi preciso que criassem mais um conjunto numérico, esse seria um pouco diferente dos outros, pois iria conter em sua estrutura a letra i. Sua representação é feita pela letra maiúscula C.

Esse conjunto é chamado de conjunto dos números complexos, veio pra resolver raízes com índices pares e radicando negativo, pois no conjunto dos reais essa operação não teria solução.

Podemos concluir que o conjunto dos números reais está contido no conjunto dos números complexos.

ARTIGOS DE "Conjunto dos números complexos"

Conjugado

Para determinarmos o oposto, o conjugado e a igualdade de qualquer número complexo precisamos conhecer alguns fundamentos.

Oposto

O oposto de qualquer número real é o seu simétrico, o oposto de 10 é -10, o oposto de -5 é +5. O oposto de um número complexo respeita essa mesma condição, pois o oposto do número complexo z será – z.

Por exemplo: Dado o número complexo z = 8 – 6i, o seu oposto será:
- z = - 8 + 6i.

Conjugado

Para determinarmos o conjugado de um número complexo, basta representar o número complexo através do oposto da parte imaginária. O conjugado de z = a + bi será:



Exemplo:
z = 5 – 9i, o seu conjugado será:

z = – 2 – 7i, o seu conjugado será

Igualdade

Dois números complexos serão iguais se, e somente se, respeitarem a seguinte condição:
Partes imaginárias iguais
Partes reais iguais

Dado os números complexos z1 = a + bi e z2 = d + ei, z1 e z2, serão iguais se, somente se, a = d e bi = ei.


Observações:

A soma de números complexos opostos será sempre igual a zero.
z + (-z) = 0.

O conjugado do conjugado de um número complexo será o próprio número complexo.


Não existe relação de ordem no conjunto dos números complexos, então não podemos estabelecer quem é maior ou menor.

Exemplo 1

Dado o número complexo z = - 2 + 6i, calcule o seu oposto, o seu conjugado e o oposto do conjugado.

Oposto
- z = 2 - 6i

Conjugado


Oposto do conjugado



Exemplo 2

Determine a e b de modo que .

-2 + 9i = a - bi

Precisamos estabelecer a propriedade da relação de igualdade entre eles. Então:

a = - 2
b = - 9

Operação de numeros complexos

Quatro Operações com Complexos

Consideremos os números complexos z₁ = a + bi e z₂ = c + di ou, na forma trigonométrica,
z₁ = r₁cisq₁ e z₂ = r₂cisq₂

• Adição

Algebricamente, a soma é na forma:  z₁ + z₂ = a + c + (b + d)i

Na notação trigonométrica não há como simplificar.

De notar que, se z e w forem dois complexos: z + w = w + z.

Considerando os números como vectores, geometricamente, a soma de complexos não passa da soma dos vectores que os representam pela "regra do paralelogramo".

• Subtracção

A subtracção de z₁ por z₂ não é mais que a soma de z₁ com o simétrico de z₂, ou seja,  
z₁ - z₂ = z₁ + (-z₂).

Geometricamente, considerando os números como vectores, a subtracção corresponde à adição do primeiro vector com o simétrico do segundo vector.

• Produto

O produto de z₁ por z₂ é o número complexo
z₁.z₂ = (ac - bd) + (ad + cb)i

 ou, na forma trigonométrica  z₁.z₂ = r₁r₂cis(q₁ + q₂) 

Vejamos a interpretação geométrica do produto de dois complexos, z₁ = a + ib e z₂ = c + id. Esta operação não corresponde, directamente, a nenhuma operação conhecida entre vectores.

Suponhamos que z₂ é um número real, isto é, que d = 0; então o produto de z₁ por z₂ corresponde ao produto do vector (a, b) pelo número real c. Se c>0, então esta operação corresponde a uma dilatação de razão c do vector z₁ e se c<0 corresponde a uma dilatação de razão |c| do mesmo vector, seguida de uma rotação de 180º de centro na origem.

Consideremos, agora, que z₂ = i. Neste caso o produto do complexo a + bi por i corresponde à rotação de 90º no sentido directo (contrário ao movimento dos ponteiros do relógio) e em torno da origem do vector (a, b), obtendo-se o vector (-b, a).

O produto de um complexo a + bi por um imaginário puro ki combina as duas operações anteriores: o produto do vector (a, b) por k, seguido de uma rotação de 90º no sentido directo em torno da origem do vector obtido.

Estas operações podem ser facilmente visualizadas na figura seguinte:

Vejamos agora o produto de um complexo a + bi pelo complexo c + di. Este produto é equivalente a c Ž (a + bi) + di Ž (a + bi), por isso vectorialmente corresponde a:

1. determinar o produto do vector (a,b) pelo número real c;	2. determinar o produto do vector (a, b) pelo número real d e fazer uma rotação de 90º ao vector obtido
3. adicionar os vectores obtidos em 1. e 2.

• Divisão 

O quociente entre z₁ e z₂ é o produto de z₁ pelo inverso de z₂, ou seja, z₁/z₂ = z₁.z₂^-1 

Na prática, basta multiplicar e dividir z₁ por z₂ 

Aplicação de numeros complexos 2ª parte

Potencia de 1 + i

Os números considerados complexos são escritos acompanhados de uma parte imaginária. No complexo z = a + bi, temos que a parte imaginária é representada por bi. Considerando i a unidade imaginária, vamos determinar alguns valores de in. Veja:

Qualquer número elevado a zero será sempre 1, então:
i ⁰ = 1

Qualquer número elevado a 1 será ele mesmo, então:
i ¹ = i

Conforme a regra dos números complexos:
i ² = – 1
i ³ = i² * i = (–1) * i = –i
i ⁴ = i² * i² = (–1) * (– 1) = 1
i ⁵ = i⁴ * i = 1 * i = i
i ⁶ = i⁵ * i = i * i = i² = –1
i ⁷ = i⁶ * i = (–1) * i = – i
i ⁸ = i⁴ * i⁴ = 1 * 1 = 1
i⁹ = i⁸ * i = 1 * i = i
i¹⁰ =(i²)⁵ = (–1)⁵ = –1

A partir da potência i4 as outras vão se repetindo de 4 em 4, para calcularmos in (n um número inteiro qualquer), para calcularmos por exemplo a potência i343, iremos dividir o expoente n por 4. No caso do exemplo, iremos dividir 343 por 4, irá sobrar um resto r igual a 3, assim, podemos concluir que:

i ⁿ = i ^r
i ³⁴³ = i³, portanto i³⁴³ = – i

Exemplo 1

Aplicando as propriedades da potência, calcule (2 – 2i)⁶.
Podemos fatorar o expoente da seguinte forma:

[(2 – 2i)²]³ =
[2² – 2 * 2 * (2i) + (2i)²]³
[4 – 8i + 4i²]³ =
[4 – 8i + 4 * (–1)]³ =
[4 – 8i – 4]³ =
[– 8i]³ =
– 512 * i³ =
– 512 * (– i) =
+ 512i

Exemplo 2

Para calcularmos a seguinte soma: i 1993 + i 1994 + i 1995, devemos dividir cada expoente por 4 utilizando da seguinte propriedade i ⁿ = i ^r.
Dividindo 1993 por 4, termos como resto 1; dividindo 1994 por 4, teremos resto 2; dividindo 1995 por 4, teremos resto 3, substituindo os expoentes 1993, 1994 e 1995 (aplicando a propriedade in = ir) pelos seus respectivos restos, teremos:

i¹ + i² + i³ =
i + (–1) + (–i) =
i – 1 – i =
– 1 + i – i =
– 1

Portanto, i¹⁹⁹³ + i¹⁹⁹⁴ + i¹⁹⁹⁵ = –1. 

Plano de Gauss

Por volta do século XV, os matemáticos tinham um único pensamento: "O quadrado de um número positivo, bem como o de um número negativo, é positivo. Um número negativo não é quadrado de nenhum número, pois não existe raiz quadrada de um número negativo”.
Raízes quadradas de números negativos continuavam aparecendo, e o que mais preocupava os matemáticos da época era que essas raízes, sendo desenvolvidas de acordo com as regras algébricas, forneciam resultados satisfatórios, que não podiam ser obtidos de outra forma.
Foi através de estudos relacionados aos matemáticos Wessel, Argand e Gauss, que muitos resolveram associar os números a e b de um complexo a coordenadas de um ponto no plano, criando assim uma representação geométrica para um complexo.

A criação dos números complexos revolucionou, de certa forma, a Matemática, pois se criava mecanismos para obtenção de resultados envolvendo a raiz quadrada de um número negativo, até então um mistério. Os complexos são formados por uma parte real (x) e outra imaginária (y), assumindo a seguinte forma algébrica: z = x + yi. O número complexo pode ser representado no plano através de um ponto Q de coordenadas (x, y), sobre o eixo x marcamos a parte real e sobre o eixo y a parte imaginária de z. O ponto Q deve receber o nome de afixo ou imagem geométrica de z.



Representando geometricamente um número complexo

a) z = 1 + i, A(1,1)
b) z = 3 + 2i, B(3,2)
c) z = -2 + 4i, C(-2,4)
d) z = -3 -4i, D(-3,-4)
e) z = 2 + 2i, E(2,2)
f) z = 4i, F(0,4)
g) z = -5, G(-5,0)

Questões:

01. O produto (5 + 7i) (3 - 2i) vale:

a) 1 + 11i
b) 1 + 31i
c) 29 + 11i
d) 29 - 11i
e) 29 + 31i


02. Se f(z) = z² - z + 1, então f(1 - i) é igual a:

a) i
b) -i + 1
c) i - 1
d) i + 1
e) -i


03. (FUVEST) Sendo i a unidade imaginária (i² = -1) pergunta-se: quantos números reais a existem para os quais (a + 1)⁴ é um número real?

a) 1
b) 2
c) 3
d) 4
e) infinitos

 
04.  Sendo i a unidade imaginária o valor de i¹⁰ + i^-100 é:

a) zero
b) i
c) -i
d) 1
e) -1

 
05. Sendo i a unidade imaginária, (1 - i )^-2 é igual a:

a) 1
b) -i
c) 2i
d) -i/2
e) i/2


06. A potência (1 - i )¹⁶ equivale a:

a) 8
b) 16 - 4i
c) 16 - 16i
d) 256 - 16i
e) 256


07. Se os números complexos z1 = 2 - i e z2 = x + 1, x real e positivo, são tais que |z₁ . z₂|² = 10 então x é igual a: 

a) 5
b) 4
c) 3
d) 2
e) 1


08. O módulo do complexo cos a - i . sen a é:

a) -1
b) -i
c) i
d) i4
e) i5


09. Calcular as raízes quadradas do número complexo 5 - 12i.


10. Achar o conjunto-verdade, em R, da equação x⁸ - 17x⁴ + 16 = 0.



Resolução:

01. C	02. C	03. C	04. A
05. E	06. E	07. E	08. D

 09. 3 - 2i; -3 + 2i

10. V = {1, i, -1, -i, 2, 2i, -2, -2i}

Aplicação de numeros complexos 3ª parte

Exercícios Resolvidos:

1) Sendo z = (m² - 5m + 6) + (m² - 1) i , determine m de modo que z seja um imaginário puro.

Solução: Para que o complexo z seja um imaginário puro, sua parte real deve ser nula ou seja, devemos ter
m² - 5m + 6 = 0, que resolvida encontramos m=2 ou m=3.

2) Determine a parte real do número complexo z = (1 + i)¹² .

Solução: Observe que (1 + i)¹² = [(1 + i)²]⁶ . Nestas condições, vamos desenvolver o produto notável
(1 + i)² = 1² + 2.i + i² = 1 + 2i -1 = 2i \ (1 + i)² = 2i (isto é uma propriedade importante, que vale a pena ser memorizada).
Substituindo na expressão dada, vem:
(1 + i)¹² = [(1 + i)²]⁶ = (2i)⁶ = 2⁶.i⁶ = 64.(i²)³ = 64.(-1)³ = - 64.
Portanto, o número complexo dado fica z = - 64 = - 64 + 0i e portanto sua parte real é igual a -64.

3) Determine a parte imaginária do número complexo z = (1 - i)²⁰⁰ .

Solução: Podemos escrever o complexo z como: z = [(1 - i)²]¹⁰⁰ . Desenvolvendo o produto notável
(1 - i)² = 1² - 2.i + i² = 1 - 2i -1 = - 2i \ (1 - i)² = - 2i (isto é uma propriedade importante, que merece ser memorizada).
Substituindo na expressão dada, vem:
z = (- 2i)¹⁰⁰ = (- 2)¹⁰⁰. i¹⁰⁰ = 2¹⁰⁰ . i¹⁰⁰ = 2¹⁰⁰ . ( i² )⁵⁰ = 2¹⁰⁰. (- 1)⁵⁰ = 2¹⁰⁰ . 1 = 2¹⁰⁰.

Logo, o número complexo z é igual a 2¹⁰⁰ e portanto um número real. Daí concluímos que a sua parte imaginária é zero. 

Exercicios 

1 - Calcule o número complexo i¹²⁶ + i^-126 + i³¹ - i¹⁸⁰

2 - Sendo z = 5i + 3i² - 2i³ + 4i²⁷ e w = 2i¹² - 3i¹⁵ ,
calcule Im(z).w + Im(w).z .

3 - UCMG - O número complexo 2z, tal que 5z + 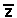= 12 + 6i é:

4 - UCSal - Para que o produto (a+i). (3-2i) seja real, a deve ser:

5 - UFBA - Sendo a = -4 + 3i , b = 5 - 6i e c = 4 - 3i , o valor de ac+b é:

6 - Mackenzie-SP - O valor da expressão y = i + i² + i³ + ... + i¹⁰⁰¹ é:

7) Determine o número natural n tal que (2i)ⁿ + (1 + i)²ⁿ + 16i = 0.
Resp: 3
Clique aqui para ver a solução.

8) Calcule [(1+i)⁸⁰ + (1+i)⁸²] : i⁹⁶.2⁴⁰
Resp: 1+2i

9) Se os números complexos z e w são tais que z = 2-5i e w = a+bi , sabendo-se que z+w é um número real e z.w .é um imaginário puro , pede-se calcular o valor de b² - 2a.
Resp: 50

10) Se o número complexo z = 1-i é uma das raízes da equação x¹⁰ + a = 0 , então calcule o valor de a.
Resp: 32i

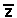
11) Determine o número complexo z tal que iz + 2 . + 1 - i = 0.

12 - UEFS-92.1 - O valor da expressão E = x^-1 + x², para x = 1 - i , é:
a)-3i
b)1-i
c) 5/2 + (5/2)i
d) 5/2 - (3/2)i
e) ½ - (3/2)i

13 -UEFS-93.2 - Simplificando-se a expressão E = i⁷ + i⁵ + ( i³ + 2i⁴ )² , obtêm-se:
a) -1+2i
b) 1+2i
c) 1 - 2i
d) 3 - 4i
e) 3 + 4i

14 - UEFS-93.2 - Se m - 1 + ni = (3+i).(1 + 3i), então m e n são respectivamente:
a) 1 e 10
b) 5 e 10
c) 7 e 9
d) 5 e 9
e) 0 e -9

15 - UEFS-94.1 - A soma de um numero complexo z com o triplo do seu conjugado é igual a -8 - 6i. O módulo de z é:
a) Ö 13
b) Ö 7
c) 13
d) 7
e) 5

16 - FESP/UPE - Seja z = 1+i , onde i é a unidade imaginária. Podemos afirmar que z⁸ é igual a:
a) 16
b) 161
c) 32
d) 32i
e) 32+16i

17 - UCSal - Sabendo que (1+i)²² = 2i, então o valor da expressão
y = (1+i)⁴⁸ - (1+i)⁴⁹ é:
a) 1 + i
b) -1 + i
c) 2²⁴ . i
d) 2⁴⁸ . i
e) -2²⁴ . i

GABARITO:

1) -3 - i   
2) -3 + 18i  
3) 4 + 3i  
4) 3/2  
5) -2 + 18i  
6) i  
7) 3  
8) 1 + 2i
9) 50  
10) 32i  
11) -1 - i
12) B   
13) D   
14) A   
15) A  
16) A   
17) E